APFC: Adaptive Particle Filter for Change Point Detection of Profile Data in Manufacturing Systems
Abstract
Change point detection is critical in quality inspection and assessment in manufacturing systems. This paper proposes an adaptive particle filter algorithm (APFC) for online change point detection in manufacturing processes. By adaptively selecting particle sizes based on change mechanisms, APFC reduces computational costs while maintaining detection accuracy. The method is validated through extensive simulations and real case studies in a pipe tightening process and a nanoparticle dispersion process.
Challenges
- Nonlinear & non-stationary signals
- Lateral oscillations (return difference)
- Varying signal lengths
Goal
Develop a generic change point detection method for the pipe-casing tightening process by considering the mechanics in torque signals.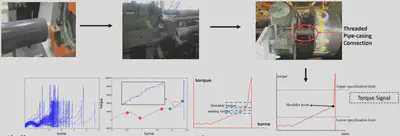
Two-Phase State Space Model
- Measurement model
$$ y_k = \begin{cases} a_t + b_k t_k + \epsilon_k & t_k < c \\ a_0 + b_0 c + b_k (t_k - c) + \epsilon_k & t_k \geq c \end{cases} \quad \left( \begin{array}{c} a_0 \\ b_0 \end{array} \right) \sim \mathcal{N}(\mu, \Sigma) $$
$$ c \sim \text{Beta}(\alpha, \beta) $$ $$ \epsilon_k \sim \mathcal{N}(0, \sigma_k^2) $$
$t_k$: turns, $c$: change point position, $t_k$ and $y_k$ are observations, $k$: time
Prediction model
$$ a_k = \begin{cases} a_{k-1} & \text{with probability } 1 - p \\ a_0 + b_0 c & \text{with probability } p \end{cases} $$
$$ b_k = \begin{cases} b_{k-1} & \text{with probability } 1 - p \\ b_{k-1} + \delta & \text{with probability } p \end{cases} $$
$$ \delta \sim \text{truncateN}( \text{range}, \sigma^2 ) $$
Juan Du
Assistant Professor
My research interests include knowledge-infused data science for quality improvement, industrial data analytics and machine learning, and system informatics and control for manufacturing applications.